Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini. Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala. Tag ini diberikan pada April 2025.

Dalam matematika, suatu barisan selang tersarang^[1], barisan selang bersarang, atau barisan selang susut^[2] dapat dipahami secara intuitif sebagai sekumpulan terurut selang-selang ${\displaystyle I_{n}}$ dengan bilangan asli ${\displaystyle n}$ sebagai indeks. Suatu barisan selang ${\displaystyle \langle I_{n}\rangle }$ disebut sebagai selang bersarang jika memenuhi dua kondisi berikut:

1. Setiap selang pada barisan akan termuat pada selang sebelumnya. Secara simbolis, maka ${\displaystyle I_{n+1}\subseteq I_{n}}$ untuk setiap ${\displaystyle n\in \mathbb {N} }$
2. Panjang selangnya bisa sependek apapun (yang berarti panjangnya akan kurang dari setiap ambang batas ${\displaystyle \varepsilon }$ setelah suatu indeks ${\displaystyle N}$)

Dengan kata lain, batas kiri selang ${\displaystyle I_{n}}$ hanya dapat bertambah (${\displaystyle a_{n+1}\geq a_{n}}$) dan batas kanannya hanya dapat berkurang (${\displaystyle b_{n+1}\leq b_{n}}$).

Secara historis - jauh sebelum ada yang mendefinisikan selang bersarang dalam buku ajar - orang-orang secara implisit mengonstruksikan selang bersarang untuk perhitungan konkret. Misalnya, bangsa Babilonia kuno menemukan metode untuk menghitung akar kuadrat dari suatu bilangan. Selain itu, Archimedes mengonstruksikan barisan segi banyak yang mengapit lingkaran dengan diameter 1 satuan dari luar dan dari dalam, untuk memperoleh batas atas dan batas bawah dri keliling lingkarannya, yaitu bilangan pi ${\displaystyle \pi }$.

Seperti yang telah disinggung pada bagian pembuka dari artikel ini, selang tersarang (dan algoritma-algoritma terkait) secara historis digunakan sebagai metode untuk melakukan perhitungan spesifik. Beberapa variasi dan interpretasi modern dari teknik-teknik kuno ini diantaranya ialah:

Untuk menghitung nilai akar kudrat dari suatu bilangan ${\displaystyle x>1}$, jelas bahwa ${\displaystyle 1\leq {\sqrt {x}}\leq x}$ (yang dituliskan dalam notasi teori himpunan, maka ${\displaystyle {\sqrt {x}}\in \left[1,\,x\right]}$), sehingga dipilih selang ${\displaystyle I_{1}=\left[1,\,x\right]}$. Jika diketahui bilangan kuadrat sempurna selanjutnya (yaitu suatu ${\displaystyle k\in \mathbb {N} }$ yang memenuhi pertidaksamaan ${\displaystyle k^{2}>x}$), maka dapat dipilih selang ${\displaystyle I_{1}=\left[1,\,k\right]}$.

Selang-selang ${\displaystyle I_{n}=\left[a_{n},\,b_{n}\right]}$ lainnya (dengan ${\displaystyle n\in \mathbb {N} }$) dapat didefinisikan secara rekursif dengan membandingkan titik tengah dari ${\displaystyle I_{n}}$ (yaitu titik ${\displaystyle m_{n}={\tfrac {a_{n}+b_{n}}{2}}}$) dengan nilai ${\textstyle {\sqrt {x}}}$. Terdapat dua kasus yang perlu ditinjau, yaitu:

1. Jika ${\displaystyle (m_{n})^{2}\geq x}$, maka berlaku rantai pertidaksamaan $${\displaystyle {\begin{aligned}x&\leq (m_{n})^{2}\\{\sqrt {x}}&\leq m_{n}\\a_{n}\leq {\sqrt {x}}&\leq m_{n}\leq b_{n}\end{aligned}}}$$ sehingga pada kasus ini, dapat dipilih ${\displaystyle I_{n+1}=\left[a_{n},\,m_{n}\right]}$.
2. Jika ${\displaystyle (m_{n})^{2}\leq x}$, maka berlaku rantai pertidaksamaan $${\displaystyle {\begin{aligned}(m_{n})^{2}&\leq x\\m_{n}&\leq {\sqrt {x}}\\a_{n}\leq m_{n}&\leq {\sqrt {x}}\leq b_{n}\end{aligned}}}$$ sehingga pada kasus ini, dapat dipilih ${\displaystyle I_{n+1}=\left[m_{n},\,b_{n}\right]}$.

Kedua kasus di atas menjamin bahwa ${\displaystyle {\sqrt {x}}\in I_{n+1}}$. Melalui konstruksi ini, selang-selangnya bersarang dan panjang selang pada setiap langkah rekursinya ialah setengah panjang semula. Akibatnya, nilai batas bawah dan batas atas dari ${\textstyle {\sqrt {x}}}$ dapat mencapai sembarang tingkat keakuratan yang diperlukan (jika diberikan waktu perhitungan yang cukup).

Jika ${\displaystyle 0<y<1}$, maka ${\displaystyle {\tfrac {1}{y}}>1}$, sehingga nilai ${\displaystyle {\sqrt {y}}}$ dapat dicari dengan menggunakan algoritma di atas melalui pengubahan variabel ${\displaystyle x:={\tfrac {1}{y}}}$, lalu menghitung timbal-baliknya setelah tingkat ketelitian yang diinginkan telah tercapai.

Untuk mengilustrasikan algoritma ini, maka akan digunakan ${\displaystyle {\sqrt {5}}}$ sebagai contoh. Perhatikan bahwa ${\displaystyle 1^{2}<5<3^{2}}$, sehingga dapat didefinisikan ${\displaystyle I_{1}:=\left[1,\,3\right]}$ sebagai selang pertama, sebab ${\displaystyle {\sqrt {5}}}$ termuat pada selang tersebut. Langkah selanjutnya ialah menghitung titik tengah selang untuk menentukan apakah kuadrat nilainya kurang dari 5 atau lebih dari 5, dan memilih batas selang selanjutnya berdasarkan hasil tersebut, sebelum prosesnya diulang:

${\displaystyle n}$	${\displaystyle I_{n}}$	${\displaystyle m_{n}}$			${\displaystyle (m_{n})^{2}}$	${\displaystyle I_{n\,+\,1}}$
${\displaystyle 1}$	${\displaystyle \left[1,\,3\right]}$	${\displaystyle {\tfrac {1\,+\,3}{2}}}$	${\displaystyle =}$	${\displaystyle 2}$	${\displaystyle 4}$	${\displaystyle \left[2,\,3\right]}$
${\displaystyle 2}$	${\displaystyle \left[2,\,3\right]}$	${\displaystyle {\tfrac {2\,+\,3}{2}}}$	${\displaystyle =}$	${\displaystyle 2.5}$	${\displaystyle 6.25}$	${\displaystyle \left[2,\,2.5\right]}$
${\displaystyle 3}$	${\displaystyle \left[2,\,2.5\right]}$	${\displaystyle {\tfrac {2\,+\,2.5}{2}}}$	${\displaystyle =}$	${\displaystyle 2.25}$	${\displaystyle 5.0625}$	${\displaystyle \left[2,\,2.25\right]}$
${\displaystyle 4}$	${\displaystyle \left[2,\,2.25\right]}$	${\displaystyle {\tfrac {2\,+\,2.25}{2}}}$	${\displaystyle =}$	${\displaystyle 2.125}$	${\displaystyle 4.515625}$	${\displaystyle \left[2.125,\,2.25\right]}$
${\displaystyle 4}$	${\displaystyle \left[2.125,\,2.25\right]}$	${\displaystyle {\tfrac {2.125\,+\,2.25}{2}}}$	${\displaystyle =}$	${\displaystyle 2.1875}$	${\displaystyle 4.78515625}$	${\displaystyle \left[2.1875,\,2.25\right]}$
${\displaystyle 5}$	${\displaystyle \left[2.1875,\,2.25\right]}$	${\displaystyle {\tfrac {2.1875\,+\,2.25}{2}}}$	${\displaystyle =}$	${\displaystyle 2.21875}$	${\displaystyle 4.9228515625}$	${\displaystyle \left[2.21875,\,2.25\right]}$
${\displaystyle 6}$	${\displaystyle \left[2.21875,\,2.25\right]}$	${\displaystyle {\tfrac {2.21875\,+\,2.25}{2}}}$	${\displaystyle =}$	${\displaystyle 2.234375}$	${\displaystyle 4.992431640625}$	${\displaystyle \left[2.234375,\,2.25\right]}$
${\displaystyle \vdots }$	${\displaystyle \vdots }$	${\displaystyle \vdots }$	${\displaystyle \vdots }$	${\displaystyle \vdots }$	${\displaystyle \vdots }$	${\displaystyle \vdots }$

Setiap kali titik tengah berikutnya dihitung, rentang nilai yang mungkin untuk ${\displaystyle {\sqrt {5}}}$ dapat dipersempit sehingga nilai-nilai yang terdapat pada selangnya akan semakin mendekati nilai sebenarnya dari ${\displaystyle {\sqrt {5}}}$, yaitu ${\displaystyle 2.236067977\ldots }$. Dengan kata lain, setiap perubahan beruntun dari batas selang yang memuat ${\displaystyle {\sqrt {5}}}$ akan meningkatkan presisi perkiraan nilai ${\displaystyle {\sqrt {5}}}$, baik dengan menaikkan batas bawah selangnya, maupun dengan menurunkan batas atas selangnya.

Prosedur ini dapat diulang sebanyak yang diperlukan untuk mencapai tingkat ketelitian yang diinginkan. Secara teori, maka nilai sebenarnya dari akar kuadrat ini dapat digapai dengan mengulangi langkahnya tanpa henti.

Metode Babilonia menggunakan algoritma yang lebih efisien untuk menghasilkan hampiran dari ${\textstyle {\sqrt {x}}}$ (dengan ${\displaystyle x>0}$) dengan lebih cepat. Deskripsi modern yang menggunakan selang bersarang mirip dengan algoritma di atas, namun alih-alih menggunakan barisan titik-titik tengah, barisan yang digunakan ialah ${\displaystyle \langle c_{n}\rangle }$ dengan relasi perulangan $${\displaystyle c_{n+1}:={\dfrac {1}{2}}\left(c_{n}+{\dfrac {x}{c_{n}}}\right)\qquad \qquad \forall n\in \mathbb {N} }$$ dan sembarang nilai awal ${\displaystyle c_{1}>0}$. Barisan ini menghasilkan barisan selang $${\displaystyle {\begin{aligned}I_{1}&=\left[0,\,k\right]&&k^{2}>x\\I_{n}:&=\left[{\tfrac {x}{c_{n}}},\,c_{n}\right]\end{aligned}}}$$ yang memberikan batas bawah dan batas atas yang akurat dari ${\textstyle {\sqrt {x}}}$ dengan lebih cepat. Pada penerapannya, cukup barisan ${\displaystyle \langle c_{n}\rangle }$ yang perlu diperhatikan, yang akan konvergen ke ${\textstyle {\sqrt {x}}}$ (dan begitu juga batas bawah selangnya). Algoritma ini merupakan kasus khusus dari metode Newton.

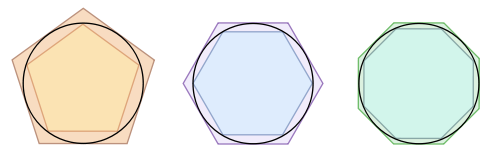
Seperti yang terlihat pada gambar di bagian kanan, batas bawah dari keliling lingkaran dapat diperoleh melalui keliling segi banyak beraturan dalam lingkaran dan batas atas dari keliling lingkaran dapat diperoleh melalui keliling segi banyak beraturan luar lingkaran. Jika lingkarannya berdiameter 1 satuan, maka berdasarkan definisi dari ${\displaystyle \pi }$ (yaitu rasio antara keliling lingkaran dengan jari-jarinya), keliling lingkarannya ialah ${\displaystyle \pi }$ satuan.

Sekitar tahun 250 SM, Archimedes menggunakan segi enam beraturan untuk mencari hampiran nilai ${\displaystyle \pi }$, yang panjang sisinya (dan akibatnya, kelilingnya) secara langsung dapat dicari dari panjang diameter lingkarannya. Selain itu, telah ditemukan cara untuk mencari panjang sisi dari segi-${\displaystyle 2n}$ beraturan dari panjang sisi segi-${\displaystyle n}$ yang telah diketahui. Dengan menggandakan banyaknya sisi dari bangun segi banyak nya hingga mencapai 96 sisi, Archimedes memperoleh pertidaksamaan ${\displaystyle {\tfrac {223}{71}}<\pi <{\tfrac {22}{7}}}$. Batas atas dari pertidaksamaan tersebut (yaitu ${\displaystyle {\tfrac {22}{7}}\approx 3.143}$ masih sering digunakan sebagai hampiran kasar namun pragmatis dari ${\displaystyle \pi }$.

Sekitar tahun 1600an, metode Archimedes masih menjadi standar emas untuk menghitung nilai ${\displaystyle \pi }$ dan pernah digunakan oleh matematikawan Belanda Ludolph van Ceulen untuk menghitung lebih dari tiga puluh digit dari ${\displaystyle \pi }$, yang memakan waktu puluhan tahun.

Penggunaan awal dari barisan selang bersarang dapat ditemukan dalam pelopor kalkulus, yaitu turunan dan pengintegralan. Dalam ilmu komputer, barisan selang bersarang digunakan untuk perhitungan numerik. Sebagai contoh, metode bagi-dua dapat digunakan untuk mencari akar dari fungsi-fungsi kontinu.

Dalam analisis matematis, selang bersarang menyediakan satu metode untuk memperkenalkan bilangan riil secara aksiomatik sebagai pelengkapan dari himpunan semua bilangan rasional, suatu hal diperlukan untuk membahas konsep dari kekontinuan dan keterdiferensialan. Secara historis, penemuan kalkulus diferensial dan integral oleh Isaac Newton dan Gottfried Wilhelm Leibniz dari akhir 1600an merupakan tantangan besar bagi para matematikawan yang mencoba untuk membuktikan metode mereka secara cermat; terlepas kesuksesannya dalam fisika, perekayasaan, dan rumpun ilmu pengetahuan lainnya. Deskripsi aksiomatik dari selang bersarang (atau aksioma lain yang setara) telah menjadi fondasi yang penting untuk pemahaman modern mengenai kalkulus.

Untuk konteks pada artikel ini, ${\displaystyle \mathbb {R} }$ yang dilengkapi dengan operasi ${\displaystyle +}$ dan ${\displaystyle \cdot }$ merupakan lapangan terurut Archimedes, yang berarti aksioma urutan dan sifat Archimedes berlaku.

Misalkan ${\displaystyle \langle I_{n}\rangle }$ menyatakan barisan selang tertutup, yaitu ${\displaystyle I_{n}=\left[a_{n},\,b_{n}\right]}$, dengan ${\displaystyle \left|I_{n}\right|:=b_{n}-a_{n}}$ menyatakan panjang selang ${\displaystyle I_{n}}$. Barisan ${\displaystyle \langle I_{n}\rangle }$ disebut sebagai barisan selang bersarang jika^[3]

1. ${\displaystyle \qquad \left(\forall n\in \mathbb {N} \right)\left(I_{n+1}\subseteq I_{n}\right)}$
2. ${\displaystyle \qquad \left(\forall \varepsilon >0\right)\left(\exists N\in \mathbb {N} \right)\left(\left|I_{N}\right|<\varepsilon \right)}$

Jika dideskripsikan dengan menggunakan kata, sifat 1 berarti selang-selangnya bersarang berdasarkan indeknya, sedangkan sifat 2 memformalkan gagasan "panjang selang yang menyusut mendekati 0", yang berarti untuk sembarang konstanta ${\displaystyle \varepsilon >0}$, dapat ditemukan suatu selang (dengan indeks ${\displaystyle N}$) yang panjangnya kurang dari bilangan ${\displaystyle \varepsilon }$. Perlu dicatat bahwa sifat 1 juga mengakibatkan setiap selang dengn indeks ${\displaystyle n>N}$ akan memenuhi pertidaksamaan ${\displaystyle \left|I_{n}\right|<\varepsilon }$.

Beberapa penulis menggunakan istilah selang susut menyebut barisan-barisan selang yang memenuhi kedua sifat di atas. Pada kasus ini, barisan selang bersarang merujuk kepada barisan yang hanya memenuhi sifat 1.

Jika ${\displaystyle \langle I_{n}\rangle }$ adalah barisan selang bersarang, maka pasti terdapat suatu bilangan riil yang termuat pada setiap selang ${\displaystyle I_{n}}$. Dalam notasi formal, aksioma ini menjamin bahwa $${\displaystyle \bigcap _{n\,=\,1}^{\infty }I_{n}\neq \varnothing }$$

1. Aksioma ini bersifat fundamental untuk bilangan riil, dalam artian bahwa irisan dari suatu barisan selang bersarang ${\displaystyle \bigcap _{n\,=\,1}^{\infty }I_{n}}$ bisa saja menghasilkan himpunan kosong, misalnya apabila hanya melibatkan bilangan rasional.
2. Aksioma ini ekuivalen dengan kewujudan dari infimum dan supremum, kekonvergenan dari barisan Cauchy, dan teorema Bolzano–Weierstrass. Ini artinya salah satu dari keempat hal tersebut harus diperkenalkan sebagai aksioma, dan tiga lainnya dapat kemudian dibuktikan sebagai teorema.

Dengan memperumum algoritma di atas untuk akar kuadrat, maka dapat dibuktikan bahwa pada bilangan riil, persamaan ${\displaystyle x=y^{k}}$ dengan ${\displaystyle k\in \mathbb {N} }$ dan ${\displaystyle x>0}$ dapat diselesaikan sebagai ${\displaystyle y={\sqrt[{k}]{x}}}$. Hal ini berarti terdapat suatu bilangan riil tunggal ${\displaystyle y>0}$ sedemikian sehingga ${\displaystyle x=y^{k}}$. Dibandingkan dengan bagian di atas, barisan yang diperoleh ialah barisan selang bersarang untuk akar ke-${\displaystyle k}$ dari ${\displaystyle x}$ (yaitu ${\displaystyle y}$) dengan memeriksa apakah titik tengah ${\displaystyle m_{n}}$ dari selang ke-${\displaystyle n}$ kurang dari atau lebih dari ${\displaystyle (m_{n})^{k}}$.

Diberikan suatu himpunan ${\displaystyle X\subseteq \mathbb {R} }$ dan suatu bilangan riil ${\displaystyle a}$ dan ${\displaystyle b}$ sedemikian sehingga berlaku $${\displaystyle b\leq x\leq a\qquad \qquad \forall x\in X}$$ Bilangan ${\displaystyle s=\sup \!\left(X\right)}$ disebut sebagai supremum dari ${\displaystyle X}$ jika

1. ${\displaystyle s}$ merupakan batas atas dari ${\displaystyle X}$, yaitu ${\displaystyle \left(\forall x\in X\right)\left(x\leq s\right)}$
2. ${\displaystyle s}$ merupakan batas atas terkecil dari ${\displaystyle A}$, yaitu ${\displaystyle \left(\forall c<s\right)\left(\exists x\in X\right)\left(c<x\right)}$

sedangkan bilangan ${\displaystyle i=\inf \!\left(X\right)}$ disebut sebagai infimum dari ${\displaystyle X}$ jika

1. ${\displaystyle i}$ merupakan batas bawah dari ${\displaystyle X}$, yaitu ${\displaystyle \left(\forall x\in X\right)\left(i\leq x\right)}$
2. ${\displaystyle i}$ merupakan batas bawah terbesar dari ${\displaystyle X}$, yaitu ${\displaystyle \left(\forall c>i\right)\left(\exists x\in X\right)\left(x<c\right)}$

Dengan sedikit modifikasi argumen, maka dapat ditunjukkan bahwa setiap himpunan tak kosong ${\displaystyle X\subseteq \mathbb {R} }$ yang terbatas ke bawah akan memiliki infimum.

Kewujudan infimum dan supremum pada himpunan terbatas merupakan akibat dari kelengkapan ${\displaystyle \mathbb {R} }$. Hal ini mengakibatkan kewujudan infimum dan supremum pada himpunan terbatas ekuivalen dengan sifat selang bersarang, yang berarti salah satu diantara kedua hal tersebut dapat diperkenalkan sebagai sebuah aksioma.

Setelah mendefinisikan kekonvergenan dan titik akumulasi dari suatu barisan secara formal, maka teorema Bolzano–Weierstrass dapat dibuktikan dengan menggunakan selang bersarang. Selanjutnya, fakta bahwa barisan Cauchy bersifat konvergen (dan setiap barisan konvergen merupakan barisan Cauchy) dapat dibuktikan. Hal ini kemudian menjadi bukti sifat kelengkapan di atas, yang menunjukkan ekuivalensi antara kewujudan dari infimum dan supremum, sifat selang bersarang, kekonvergenan dari barisan Cauchy, dan teorema Bolzano–Weierstrass.

Tanpa menjelaskan apa yang dimaksud dari kata "selang" ${\displaystyle I_{n}}$, hasil irisan ${\displaystyle \bigcap _{n\,=\,1}^{\infty }I_{n}}$ (yaitu himpunan seluruh titik yang termuat pada setiap selang) mungkin saja himpunan kosong ${\displaystyle \varnothing }$, suatu titik pada garis bilangan (yang dikenal dengan istilah singleton) ${\displaystyle \left\{x\right\}}$, atau suatu selang.

Kemungkinan dari irisan kosong dapat diilustrasikan melalui barisan selang terbuka berikut: $${\displaystyle I_{n}=\left(0,\,{\tfrac {1}{n}}\right)=\left\{x\in \mathbb {R} \mid 0<x<{\tfrac {1}{n}}\right\}}$$ Pada kasus ini, irisan ${\displaystyle \bigcap _{n\,=\,1}^{\infty }I_{n}}$ merupakan himpunan kosong, sebab untuk sembarang ${\displaystyle x>0}$, terdapat suatu ${\displaystyle n\in \mathbb {N} }$ sedemikian sehingga berlaku ${\displaystyle {\tfrac {1}{n}}<x}$, yaitu sembarang nilai ${\displaystyle n}$ yang memenuhi pertidaksamaan ${\displaystyle n>{\tfrac {1}{x}}}$^[4]. Akibatnya, sekecil apapun nilai ${\displaystyle x>0}$ nya, terdapat suatu selang ${\displaystyle I_{n}}$ pada barisan, sedemikian sehingga ${\displaystyle x\not \in I_{n}}$, yang mengakibatkan hasil irisannya haruslah kosong.

Keadaan tersebut berubah jika selang ${\displaystyle I_{n}}$ merupakan selang tertutup, misalnya $${\displaystyle I_{n}=\left[0,\,{\tfrac {1}{n}}\right]=\left\{x\in \mathbb {R} \mid 0\leq x\leq {\tfrac {1}{n}}\right\}}$$ Jika ${\displaystyle x>0}$, maka terdapat suatu selang pada barisan ${\displaystyle \langle I_{n}\rangle }$ yang tidak memuat ${\displaystyle x}$, tetapi untuk ${\displaystyle x=0}$, pertidaksamaan ${\displaystyle 0\leq x\leq {\tfrac {1}{n}}}$ bernilai benar untuk setiap ${\displaystyle n\in \mathbb {N} }$. Dalam kasus ini, maka ${\displaystyle \bigcap _{n\,=\,1}^{\infty }I_{n}=\left\{0\right\}}$.

• Bagi-dua
• Teorema irisan Cantor

• Fridy, J. A. (2000), "3.3 The Nested Intervals Theorem", Introductory Analysis: The Theory of Calculus, Academic Press, hlm. 29, ISBN 9780122676550 .
• Shilov, Georgi E. (2012), "1.8 The Principle of Nested Intervals", Elementary Real and Complex Analysis, Dover Books on Mathematics, Courier Dover Publications, hlm. 21–22, ISBN 9780486135007 .
• Sohrab, Houshang H. (2003), "Theorem 2.1.5 (Nested Intervals Theorem)", Basic Real Analysis, Springer, hlm. 45, ISBN 9780817642112 .
• Königsberger, Konrad (2003), "2.3 Die Vollständigkeit von R (the completeness of the real numbers)", Analysis 1, 6. Auflage (6th edition), Springer-Lehrbuch, Springer, hlm. 10-15, doi:10.1007/978-3-642-18490-1, ISBN 9783642184901